文本：回归闭式解

正如你在上个视频看到的，在求回归解时，我们会想最小化下列函数：

\sum\limits_{i=1}^n(y_i - \hat{y}_i)^2

看来，为了最小化该函数，我们需要列出等式来求截距和斜率。

比如你得到了如图的一系列数值点：

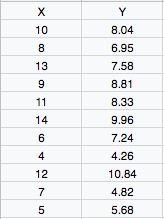
为了得到斜率和截距，我们需要进行如下计算：

\bar{x} = \frac{1}{n}\sum x_i

\bar{y} = \frac{1}{n}\sum y_i

s_y = \sqrt{\frac{1}{n-1}\sum\limits(y_i - \bar{y})^2}

s_x = \sqrt{\frac{1}{n-1}\sum\limits(x_i - \bar{x})^2}

r = \frac{\sum\limits_{i=1}^n(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum(x_i - \bar{x})^2}\sqrt{\sum(y_i - \bar{y})^2}}

b_1 = r\frac{s_y}{s_x}

b_0 =\bar{y} - b_1\bar{x}

虽然你现在完全能进行这些步骤……

但在计算机时代，全部都用手工计算实在没有必要，利用好计算机，我们就能集中精力来解释结果并根据结果进行决策，如果你想观察 Excel 是怎么一步步进行这些计算的，那你可以看这里，在接下来的课程中，你将在 Python 里做些相关练习。